• Bienvenida



      Presentación del curso

      Bienvenido a tu curso virtual de Pensamiento matemático I, donde encontrarás diversas actividades que te ayudarán a lograr las habilidades relacionadas con la observación, la intuición, la capacidad de conjeturar, la argumentación, la comunicación y socialización de inquietudes intelectuales y soluciones a problemas, así como la descripción de fenómenos o situaciones mediante el empleo del lenguaje matemático. También desarrollaras un estilo de pensamiento que te permita movilizar conocimientos previos de matemáticas, relacionar las áreas de conocimiento con otros recursos del MCCEMS, tomar mejores decisiones y utilizarlo para comprender e interactuar con el mundo que te rodea ya que se aplica en temas realmente apasionantes de nuestra vida cotidiana.

      El pensamiento matemático 1, es un recurso sociocognitivo que promueve lograr una formación humana e integral para todas y todos, deja de ser únicamente un conjunto de algoritmos que muchas veces son aplicados de manera mecánica y descontextualizada, para convertirse en un medio a través del cual pueda trabajar en la adquisición y mejoramiento de habilidades y destrezas del pensamiento tales como observar, intuir, conjeturar, argumentar, la capacidad para modelar y entender, a través del lenguaje matemático, algunos fenómenos sociales, naturales e incluso de su vida personal.



      Propósito del curso sociocognitivo

      Integrar a la matemática y al pensamiento matemático como un recurso sociocognitivo de tal forma que el desarrollo de habilidades cognitivas e incluso socioemocionales relacionadas con el pensamiento matemático se lleve a cabo a través del estudio y consideración de contenido que resulte significativo para el estudiantado.

       

      Apoyar al estudiantado en la explicación del mundo y de su entorno inmediato.

       

      Considerar el desarrollo del pensamiento matemático como un proceso no necesariamente lineal, posiblemente en espiral, complejo en donde ocurren avances, paradas, rodeos e incluso retrocesos.

       

      Relacionar al Pensamiento Matemático con otras áreas del conocimiento y con la vida, mediante el empleo de conceptos matemáticos para “satisfacer las necesidades de la vida diaria que puede tener un ciudadano constructivo, comprometido y reflexivo” (OCDE, 2010, p. 23).



      Categorías y subcategorías del área de conocimiento




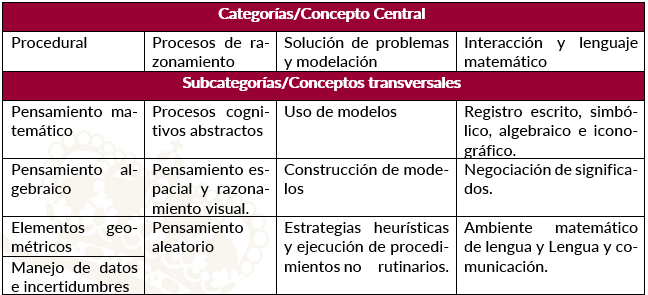
      Metas de aprendizaje



      5

      hy



      Progresiones de aprendizajes del recurso sociocognitivo

      1. Discute la importancia de la toma razonada de decisiones, tanto a nivel personal como colectivo, utilizando ejemplos reales o ficticios que sean significativos para las y los estudiantes y en los que se valore la recolección y organización de datos.

       

      2. Identifica la incertidumbre como consecuencia de la variabilidad y a través de la consulta de datos o simulaciones, considera la frecuencia con la que un evento puede ocurrir con la finalidad de tener más información sobre la probabilidad de que dicho evento suceda.

       

      3. Identifica la equiprobabilidad como una hipótesis que, en caso de que se pueda asumir, facilita el estudio de la probabilidad y observa que cuando se incrementa el número de repeticiones de una simulación, la frecuencia del evento estudiado tiende a su probabilidad teórica.

       

      4. Elige una técnica de conteo (listados, diagramas de árbol, combinaciones, ordenaciones con repetición, ordenaciones sin repetición, etc.) para calcular el número total de casos posibles y casos favorables para eventos simples con la finalidad de hallar su probabilidad y con ello generar una mayor conciencia en la toma de decisiones.

       

      5. Observa cómo la probabilidad de un evento puede actualizarse cuando se obtiene más información al respecto y considera eventos excluyentes e independientes para emplearlos en la determinación de probabilidades condicionales.

       

      6. Selecciona una problemática o situación de interés, con la finalidad de recolectar información y datos de fuentes confiables e identifica las variables relevantes para su estudio.

       

      7. Analiza datos categóricos y cuantitativos de alguna problemática o situación de interés para el estudiantado, a través de algunas de sus representaciones gráficas más sencillas como las gráficas de barras (variables cualitativas) o gráficos de puntos e histogramas (variables cuantitativas).

       

      8. Analiza cómo se relacionan entre sí dos o más variables categóricas a través del estudio de alguna problemática o fenómeno de interés para el estudiantado, con la finalidad de identificar si dichas variables son independientes.

       

      9. Analiza dos o más variables cuantitativas a través del estudio de alguna problemática o fenómenos de interés para el estudiantado, con la finalidad de identificar si existe correlación entre dichas variables.

       

      10. Cuestiona afirmaciones estadísticas y gráficas, considerando valores atípicos (en el caso de variables cuantitativas) y la posibilidad de que existan factores o variables de confusión.

       

      11. Identifica, ante la imposibilidad de estudiar la totalidad de una población, la opción de extraer información de ésta a través del empleo de técnicas de muestreo, en particular, valora la importancia de la aleatoriedad al momento de tomar una muestra.

       

      12. Valora las ventajas y limitaciones de los estudios observacionales y los compara con el diseño de experimentos, a través de la revisión de algunos ejemplos tomados de diversas fuentes.

        

      13. Describe un fenómeno, problemática o situación de interés para el estudiantado utilizando las medidas de tendencia central (media, mediana y moda) y de dispersión (desviación estándar, varianza, rango intercuartil, etc.) adecuadas al contexto y valora que tipo de conclusiones puede extraer a partir de dicha información.

       

      14. Explica un evento aleatorio cuyo comportamiento puede describirse a través del estudio de la distribución normal y calcula la probabilidad de que dicho evento suceda.

       

      15. Valora la posibilidad de hacer inferencias a partir de la revisión de algunas propiedades de la distribución normal y del sentido de la estadística inferencial para considerar algunos fenómenos que pueden modelarse con dicha distribución.



      Aprendizajes de trayectoria

      3



      Programa de trabajo aula, escuela y comunidad

      Proposito: Elaborar  de manera individual una historieta digital que plantee formas de integrarse con seguridad en ambientes virtuales para prevenir la violencia digital en el ciberespacio.


      * En caso de Pensamiento Matemático será mediante la recolección de información sobre la violencia digital empleando alguna técnica de recolección de datos.



      Evaluación

      PM2



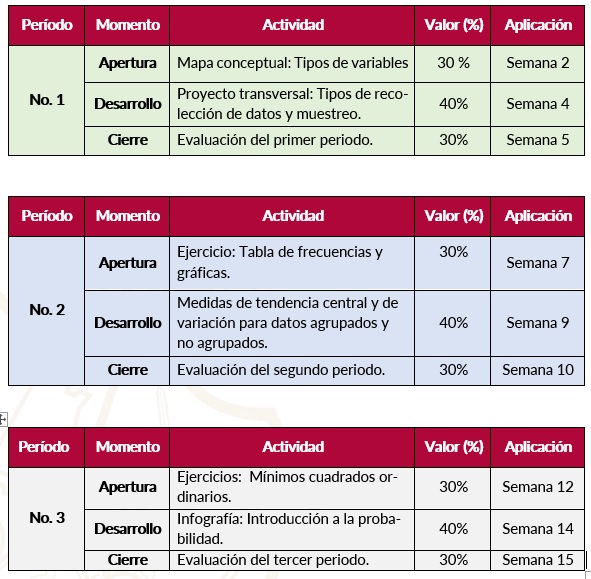
      Información general del curso



      Bibliografía

      Fuentes básicas

      • Sánchez Sánchez, Ernesto & Inzunza Cazares, Santiago.  Probabilidad y Estadística I. Primera Edición. México. Grupo Editorial Patria. ISBN: 978-6075502083.
      • Gutiérrez, Banegas. (2018). Probabilidad y Estadística. Segunda Edición. México. McGraw-Hill. ISBN: 978-1456263126.
      • Devore, Jay L. (2019). Introducción a la Probabilidad y Estadística. Primera Edición. México. Cengage Learning. ISBN: 978-6075267883.

      Fuentes complementarias

      • Salazar Guerrero, Ludwing Javier. (2021). Probabilidad y Estadística Para Bachilleratos Tecnológicos. Segunda edición. México. Grupo Editorial Patria. ISBN: 978-6077449188.

             Fuentes complementarias

       
    • Avisos Avisos

    • Actividades del Curso

  • Periodo 3

    • Introducción

      En este periodo trabajaras en la búsqueda de la correlación de variables, ver si existe una dependencia entre ellas, de igual manera analizaras las definiciones más importantes de probabilidad.

      Categorías

      C1 Procedural

      C2 Procesos de razonamiento

      C3 Interacción del lenguaje matemático

      C4 Interacción del lenguaje matemático

      Subcategorías

      • Pensamiento aritmético
      • Pensamiento algebraico
      • Procesos cognitivos abstractos
      • Pensamiento espacial y razonamiento visual
      • Pensamiento aleatorio
      • Uso de modelos
      • Registro escrito, simbólico, algebraico e iconográfico


      Metas de aprendizaje

      • Ejecuta cálculos y algoritmos para resolver problemas matemáticos y de otras áreas del conocimiento.
      • Comprueba los procedimientos usados en la resolución de problemas matemáticos y de otras áreas del conocimiento, mediante la verificación directa o empleando recursos tecnológicos o la interacción con sus pares.
      • Observa y obtiene información de una situación o fenómeno (natural o social) para establecer estrategias o formas de visualización que ayuden a explicarlo.
      • Desarrolla la percepción y la intuición para generar una hipótesis inicial ante situaciones que requieren explicación o interpretación.
      • Compara hechos, opiniones o afirmaciones categóricas o la posibilidad de ocurrencia de eventos para establecer similitudes y diferencias, organizándolos en formas lógicas o convenientes útiles en la solución de problemas.

      • Combina diferentes procesos de razonamiento matemático al plantear un modelo o resolver un problema o una situación o fenómeno natural, experimental o social e interpreta el resultado, la predicción y/o la manera de reducir el nivel de riesgo.

      • Selecciona un modelo matemático por la pertinencia de sus variables y relaciones para explicar el fenómeno estudiado en la solución de un problema.
      • Esquematiza situaciones para su solución mediante el uso de datos numéricos, representación simbólica y conceptos matemáticos para dar un significado acorde con el contexto.

      Progresiones de aprendizaje

      2. Identifica la incertidumbre como consecuencia de la variabilidad y a través de la consulta de datos o simulaciones, considera la frecuencia con la que un evento puede ocurrir con la finalidad de tener más información sobre la probabilidad de que dicho evento suceda.

      3. Identifica la equiprobabilidad como una hipótesis que, en caso de que se pueda asumir, facilita el estudio de la probabilidad y observa que cuando se incrementa el número de repeticiones de una simulación, la frecuencia del evento estudiado tiende a su probabilidad teórica.

      8. Analiza cómo se relacionan entre sí dos o más variables categóricas a través del estudio de alguna problemática o fenómeno de interés para el estudiantado, con la finalidad de identificar si dichas variables son independientes.

      9. Analiza dos o más variables cuantitativas a través del estudio de alguna problemática o fenómenos de interés para el estudiantado, con la finalidad de identificar si existe correlación entre dichas variables.
    • Foro

      Foro: Introducción a la regresión lineal

    • Página

      Actividad 14. Video y cuestionario

    • Tarea

      Actividad 15. Ejercicios: Mínimos cuadrados ordinarios.

    • Página

      Actividad 16. Video y actividad interactiva

    • Tarea

      Actividad 17. Infografía: Introducción a la probabilidad.

    • Examen

      Evaluación. Periodo 3

    • Tarea

      Portafolio de evidencias

    • Hasta aquí Pensamiento matemático I, Nos vemos en la siguiente asignatura

      ¡Te esperamos!