-
Bienvenida
Presentación del curso
Estimados estudiantes bienvenidos a la unidad de aprendizaje curricular “Pensamiento Matemático II” la cual pertenece a segundo semestre, esta será una nueva experiencia en la que aprenderemos juntos.
La clase se desarrollará en la plataforma virtual de Moodle, en donde están alojadas todas las actividades que tienes que realizar, recursos visuales, actividades de apoyo y materiales didácticos que te servirán para tu proceso de aprendizaje.
Propósito del área de conocimiento
El pensamiento matemático, en el MCCEMS, posibilita:
• Favorecer en el estudiantado el desarrollo de habilidades relacionadas con la observación, la intuición, la capacidad de conjeturar, la argumentación, la comunicación y socialización de inquietudes intelectuales y soluciones a problemas, así como la descripción de fenómenos o situaciones mediante el empleo del lenguaje matemático.
• Recuperar una perspectiva histórico-filosófica para ver a la matemática a partir de los contextos que dieron origen a los conceptos y procedimientos, de la integración de procesos de abstracción, argumentación y otros, dando un enfoque amplio contrario al enfoque mecanicista que anula la relevancia de la matemática.
• Responder a motivaciones que pueden estar en el ambiente natural, social, cultural o en el sujeto pensante, para ampliar la visión de la matemática considerando su papel transformador, su dimensión cultural e intelectual que favorezca la formación integral del ser humano.
• Dar un sentido holístico a la formación matemática en la EMS para que el estudiantado alcance una educación de calidad, que incluya contenidos relevantes, actividades pertinentes y retadoras para lograr que le dé seguridad para tomar decisiones, favorezca una postura crítica y un estado emocional que lo impulse hacia el aprendizaje permanente y desarrolle una postura crítica en un marco de respeto a la condición y dignidad humana.
• Incorporar una visión centrada en el estudiante de tal forma que la articulación de saberes, conocimientos y habilidades tenga como eje director el progreso del estudiantado, respetando siempre la coherencia y consistencia de la disciplina.
Relacionar al Pensamiento Matemático con otras áreas del conocimiento y con la vida, mediante el empleo de conceptos matemáticos para “satisfacer las necesidades de la vida diaria que puede tener un ciudadano constructivo, comprometido y reflexivo” (OCDE, 2010, p. 23).
Conceptos centrales y conceptos transversales del área de conocimiento:
Metas de aprendizaje
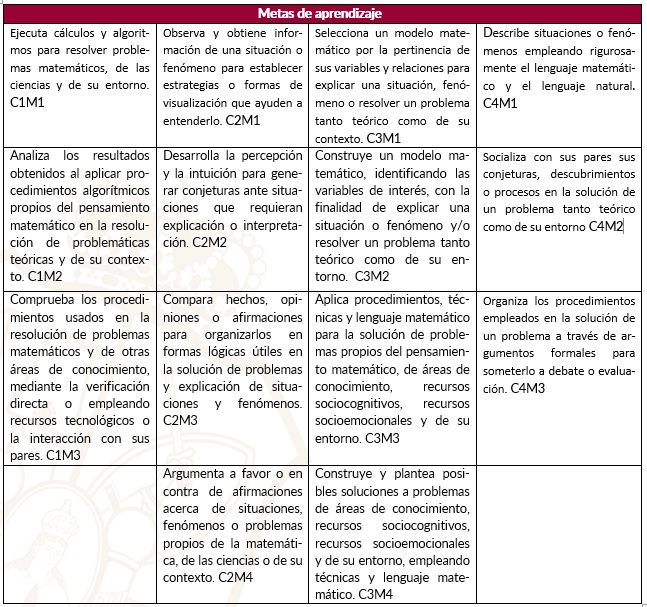
Progresiones de aprendizajes del recurso sociocognitivo

Aprendizajes de trayectoria

Evaluación
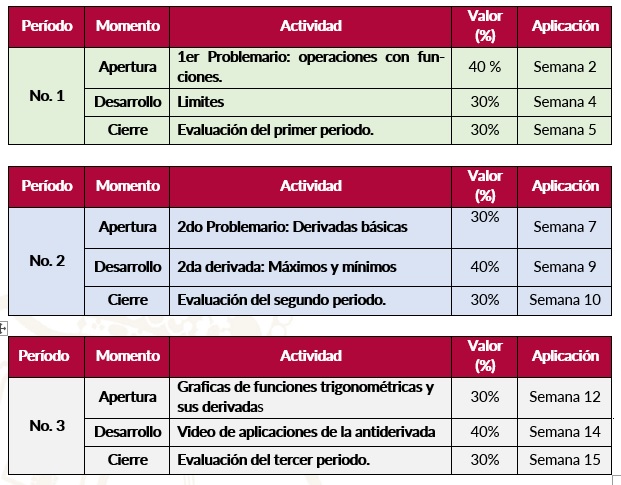
Información general del curso
Bibliografía
Fuentes básicas
- Lechuga Marrufo, Sarahi – Esparza puga, Danelly Susana. (2024). Pensamiento matemático 3. Primera edición. México. Grupo Editorial Patria. ISBN: 978- 6075744025.
- Romano Velázquez, Faustino Agustín. (2024). Pensamiento matemático III. Primera edición. México. Grupo editorial Mx. ISBN: 9786078966110.
- Guerra González, José Antonio- Sinhué Moisés, Gaytán García. (2024). Pensamiento Matemático 3, serie trayectos. Primera edición. México. Editorial Esfinge. ISBN: 978- 6071016836.
Fuentes complementarias
- Flores Cortes, Verónica. (2024). Pensamiento Matemático III. Primera edición. México. Editorial Cengage learning. ISBN: 978- 6075702247.
- Cuellar Carvajal, José Antonio. (2024). Pensamiento matemático 3. Primera edición. México. Editorial McGraw-Hill Educator. ISBN: 978-6071522986.
- Estrada, Rosa - Manuel Rene. (2019). Matemáticas 4. Edición estándar. México. Editorial Pearson. ISBN: 978-6073247566.
- CONAMAT. (2016). Cálculo diferencial e integral. Edición estándar. México. Editorial Pearson. ISBN:978-6073235853
Fuentes electrónicas
-
-
Actividades del Curso
-
Periodo 2
-
Periodo 2
-
Introducción
En este segundo periodo, se trabajarán cinco progresiones de la UAC pensamiento matemático III, en las cuales el estudiante conocerá el origen y la historia del cálculo, las principales definiciones y conceptos de la derivada, también resolverá derivadas de funciones aplicando fórmulas de sumas, productos y cociente, siendo clave en el desarrollo del estudiante observando la importancia y aplicación de la derivada en las ciencias y en la vida cotidiana, así que adentrémonos en el estudio de esta interesante sección.
Metas de aprendizaje
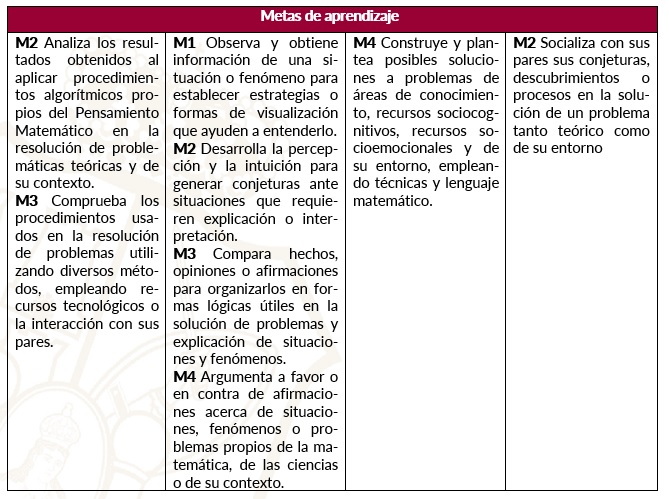
Progresiones de aprendizaje
6. Identifica y contextualiza la continuidad de funciones utilizadas en la modelación de situaciones y fenómenos y hace un estudio, utilizando el concepto de límite, de las implicaciones de la continuidad de una función tanto dentro del desarrollo matemático mismo, como de sus aplicaciones en la modelación. (C2M1, C4M2).
7. Interpreta, a partir de integrar diferentes perspectivas y métodos, el concepto central del cálculo diferencial, “la derivada”, de forma intuitiva e intenta dar una definición formal, así como la búsqueda heurística para encontrar la derivada de la función constante, lineal y algunas funciones polinomiales. (C1M2, C2M2).
8. Encuentra de manera heurística algunas reglas de derivación como la regla de la suma, la regla del producto, la regla del cociente y la regla de la cadena y las aplica en algunos ejemplos. (C2M3, C3M4).
9. Selecciona una problemática en la que el cambio sea un factor fundamental en su estudio para aplicar el concepto de la derivada como razón de cambio instantánea. (C2M2).
10. Explica y socializa el papel de la derivada para analizar una función (donde crece/decrece, máximo/mínimos locales, concavidades) y traza su gráfica. (C1M3, C2M4, C4M2)
-
-
-
-
-
-
-